Tag: fine-scale population structure

Updates to ASoSaH: new maps, updated PCA, and added newest research papers

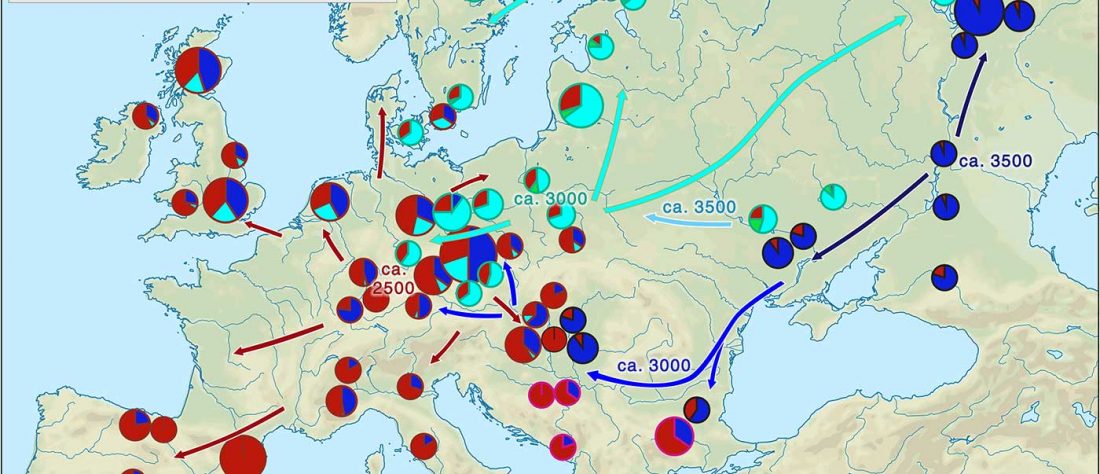
steppe-ancestry-cut

The title says it all. I have used some free time to update the series A Song of Sheep and Horses:

I basically added information from the latest papers published, which (luckily enough for me) haven’t been too … Read the rest “Updates to ASoSaH: new maps, updated PCA, and added newest research papers”

Contrastive principal component analysis (cPCA) to explore patterns specific to a dataset

Interesting open access paper Exploring patterns enriched in a dataset with contrastive principal component analysis, by Abid, Zhang, Bagaria & Zou, Nature Communications (2018) 9:2134.

Abstract (emphasis mine):

Visualization and exploration of high-dimensional data is a ubiquitous challenge across disciplines. Widely used techniques such as principal component analysis (PCA) aim to identify dominant trends in one dataset. However, in many settings we have datasets collected under different conditions, e.g., a treatment and a control experiment, and we are interested in visualizing and exploring patterns that are specific to one dataset. This paper proposes a method, contrastive principal component analysis

… Read the rest “Contrastive principal component analysis (cPCA) to explore patterns specific to a dataset”